Research
Over the past decades, we have witnessed the success of classic computational paradigm based on first-principle in many physical and engineering disciplines. For example, computational fluid dynamics (CFD) has played a critical role in the application of fluid mechanics, including aerodynamic design of aircraft, combustion simulation. Yet many challenging questions still remain in the modeling and control of complex flow phenomena such as laminar-turbulence transition, noise generation in aeroacoustics. Conventional approaches rely on performing moderate (LES) to high-fidelity simulations (DNS) for insight in design, optimization and control. This cycle that relies on traditional computational science has three issues.
- First, it involves a prohibitively high computational cost and human effort in the downstream tasks: design, control and validation process (e.g., design of transonic airfoil) or in pursuing accurate models for missing physics (e.g., closure problems).
- Second, the complex flowfield from high-fidelity simulations is challenging to interpret (e.g., extracting meaningful coherent structures).
- Third, data from high-fidelity simulations and experiments are not fully exploited (beyond validation).
My research is predicated on the synthesis of traditional computational mathematics paradigms with cutting-edge techniques in deep learning to address complex challenges in aerospace engineering. The methodologies we have developed are not only targeted but also versatile, possessing the potential for application in a variety of other engineering sectors (e.g., nuclear, manufacturing). My scholarly focus is dedicated to rigorously examining the foundational elements of scientific machine learning through a multidisciplinary prism that incorporates applied mathematics, engineering physics, and machine learning disciplines. This comprehensive approach is strategically designed to address intricate nonlinear dynamical systems. Our work is fundamentally anchored in the theories of dynamical systems, deep learning algorithms, optimization techniques, and fluid mechanics.
Thrust 1: Operator-theoretic Modeling and Control of Nonlinear Dynamical Systems
Classical approach for nonlinear systems follows the geometrical approach to describe the evolution of nonlinear dynamics in the high-dimensional state-space. Alternatively, one can switch the attention to the observable on such state-space. In contrast to classical techniques, Koopman operator seeks a linear embedding of non-linear dynamical systems from high-dimensional data from either sparse experimental measurements of the system. This transforms non-linear systems into linear systems for which closed-form analytical solutions are often available. It renders a control-oriented model for any nonlinear system. As an example of “modeling for control”, one can have Koopman-based model predictive control (MPC) which converts a non-linear MPC into a much faster linear counterpart.
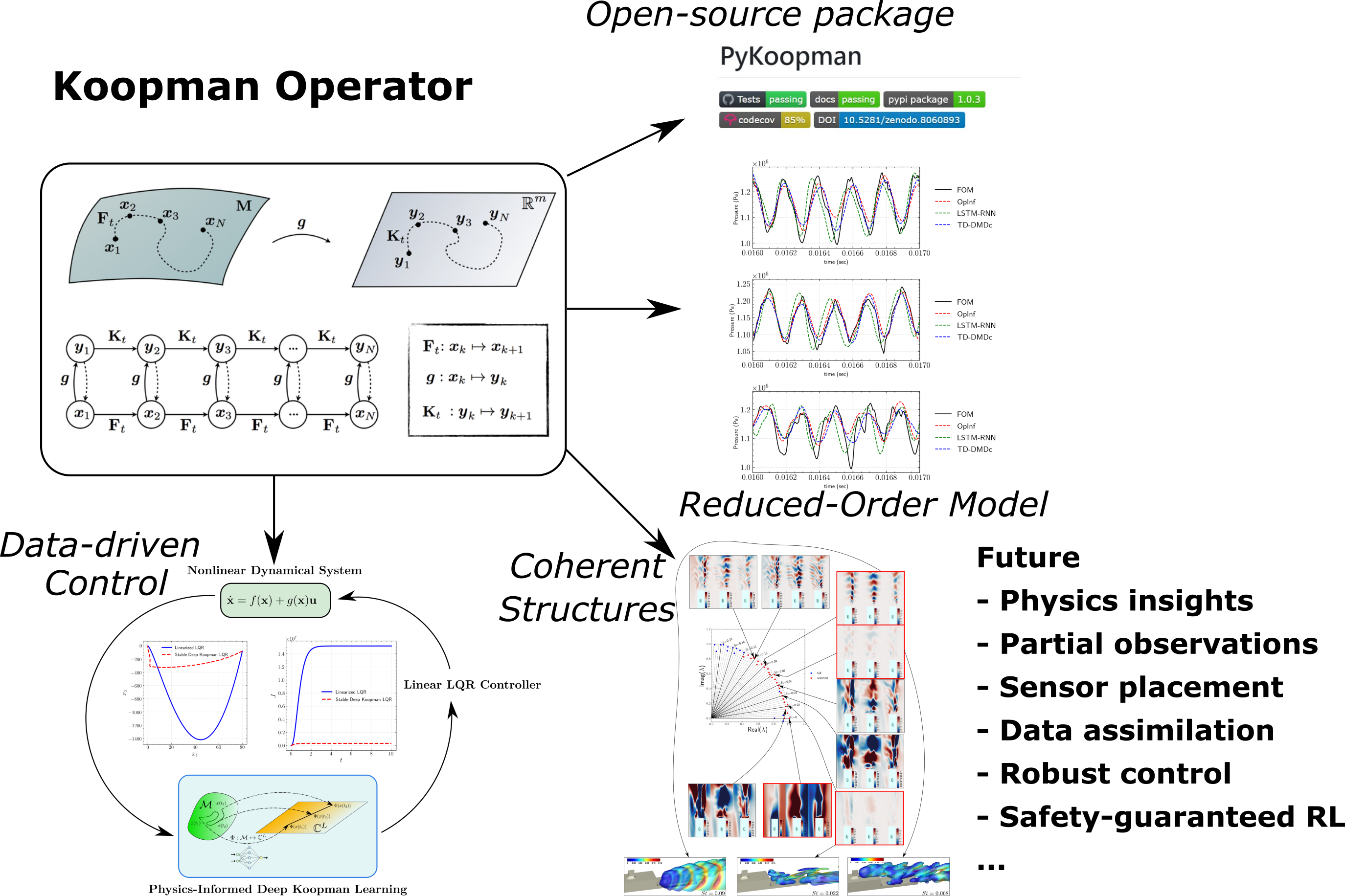
In spite of significant strides made in the theoretical exploration of the Koopman operator, the practical aspect of learning this operator from data remains an open question. Over recent years, we have pioneered a range of computational and numerical methods, complemented by theoretical insights, aimed at establishing a more robust and precise framework for learning the Koopman operator from empirical data sets. This multi-pronged approach not only enhances the accuracy of Koopman operator approximations but also fortifies its applicability across diverse scientific and engineering contexts.
Thrust 2: Predictive Reduced-Complexity Learning of Nonlinear PDE Systems
Modeling partial differential equations (PDEs) presents an elevated level of complexity compared to ordinary differential equations (ODEs), requiring not just an accurate physical modeling of multi-physics processes like fluid-structure interaction but also the crafting of computationally efficient models for high-throughput tasks such as uncertainty quantification and design optimization. Methodologically, one has the option to pursue either intrusive techniques, like reduced-order modeling, Proper Orthogonal Decomposition-Galerkin (POD-Galerkin), and Least-Squares Petrov-Galerkin (LSPG), which capitalize on known governing equations for better generalization, or non-intrusive approaches, such as machine learning surrogates and operator inference, which offer orders-of-magnitude speed-up and are hence preferred for time-sensitive, many-query situations.
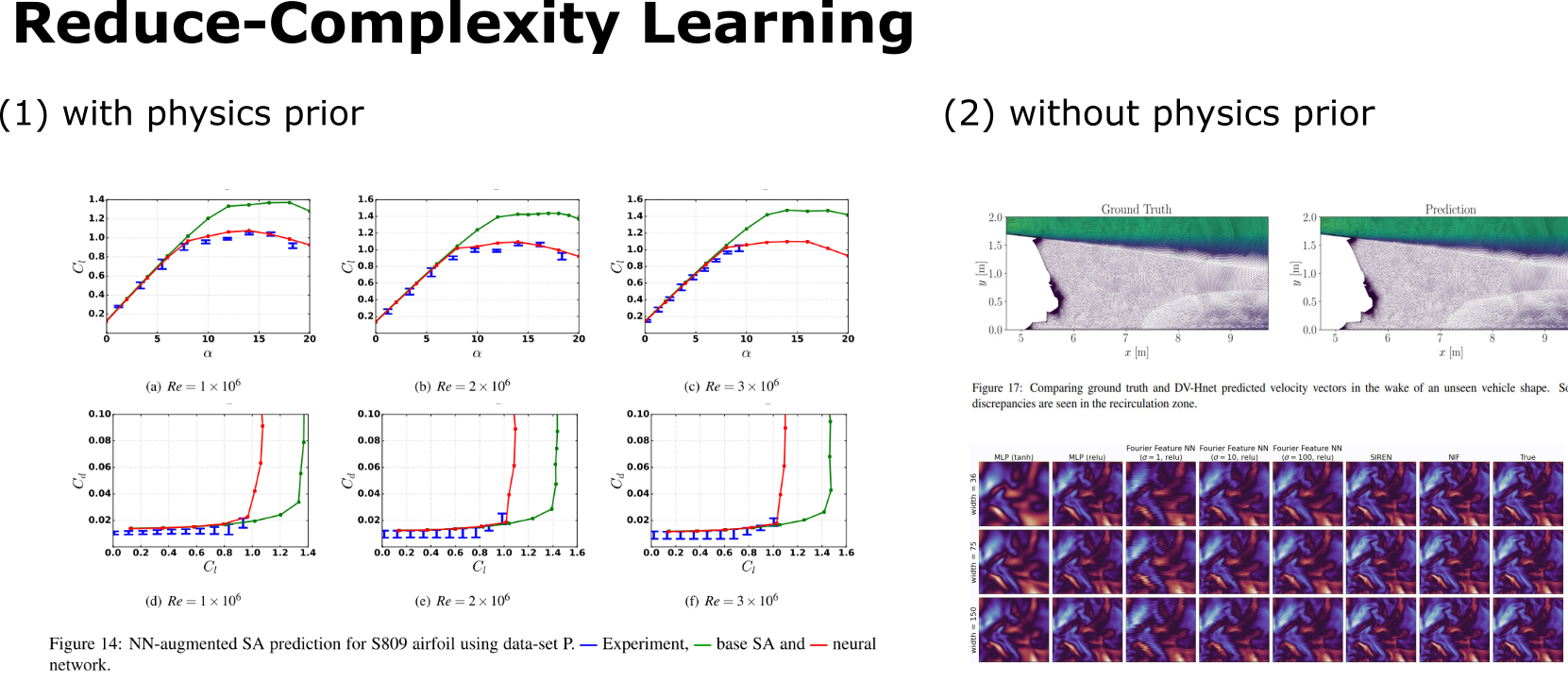
Over recent years, my team and I have developed several novel techniques, including data-driven modeling of closure dynamics, field-inversion machine learning as one of the pioneering works in differentiable physics learning, and mesh-agnostic methodologies like neural implicit flow. These methods have been validated across an array of challenging applications: Reynolds-Averaged Navier-Stokes (RANS) turbulence modeling over airfoils, sparse sensing of dynamically evolving spatial fields, and operator learning in complex, adaptively refined geometries such as flow over realistic automotive forms and the optimization of compressor airfoils. This collective body of work effectively bridges theoretical depth with practical utility, delivering nuanced solutions for modeling complex PDE systems.
